Annex I
(informative)
Conformance testing for SRF operations
This annex provides guidelines that may be useful for developing conformance requirements and conformance tests for implementation of the concepts specified in this International Standard including, but not limited to, the API specified in Clause 11.
The meaning of “error” depends on the context and application domain. Potential sources of error in SRF operations include formulation error, numerical approximation error, round-off error, truncation error and other errors associated with implementing SRF operations. In Annex B.2.3, computational error is defined to be the sum of digitization error and approximation errors made to simplify the implementation or to improve the computational efficiency of the process. Errors of this nature should not be confused with errors arising from modelling the true shape of a spatial object (celestial or abstract) by an approximate shape. In this International Standard, an ORM used to approximate the shape of an object is assumed exact. How well an ORM approximates the shape of a celestial object is outside the scope of this International Standard.
The specification of an SRF operation defines the domain and range as well as providing a functional specification of how each value in the domain is converted into a value in the range. The functional specifications are the mathematical functions in one or more variables given in Clause 10. These functional specifications include a set of rules related to the appropriate ORM, bindings to the CS, and instances related to a particular celestial object.
Each SRF operation specified in Clause 10 has a theoretically exact specification in terms of mathematical functions. These formulations are specified assuming the use of theoretically exact arithmetic (infinite precision) for developing values of an SRF operation. These exact specifications fall into one of four basic categories:
a) a finite sum of elementary mathematical functions,
b) a finite sum of quadratures,
c) an infinite iterative process, or
d) an infinite power series.
In practice, implementations that use one of these categories require the use of finite precision arithmetic along with termination in a finite number of steps or after a finite number of terms are computed. Some of the formulations may have removable singularities in the domain of a function, usually at extremes of the domain. When implementing such formulations, care should be taken in the neighbourhood of singularities to use the appropriate numerical approximations or to isolate the singular points with an open set.
This International Standard may be implemented in many different ways. Potential implementations include:
a) manual computation without using computers,
b) fixed-purpose hardware, or
c) software executing on general-purpose digital computers ranging from embedded processors to large-scale computer systems.
Given the wide range of possible implementations and the differing requirements of application domains, conformance requirements in this International Standard may be restricted to a sub-set of the domains involved. (See Annex B for a discussion of computational error and Clause 14 for specifics on conformance.)
I.5 Fundamental measure of conformance
There are several conformance criteria that are discussed in Clause 14. One fundamental measure is the numerical difference between the individual data points of an exact or reference set of points and the corresponding data points generated by a particular implementation. The absolute difference between the points in the reference data set and the corresponding points obtained from a particular implementation is referred to as a computational error. The computational error may have units of length, be angular measures or be dimensionless depending on the particular SRF operation being evaluated.
When the reference data are generated, it is assumed that computations are performed at least to double- precision as specified by IEC 60559. This means that the size of the mantissa of a floating-point number is 52 bits, which corresponds to about 15,5 decimal digits of precision (see IEC 60559:1989 [IEC 60559]). Particular implementations may not have to meet this requirement on precision but developers of the system should understand that use of lower precision arithmetic could increase the computational error when dealing with SRF operations.
I.6 Error metrics for SRF operations
An error metric is a function that allows data points developed using the exact formulations of Clause 10 to be compared to corresponding data points resulting from using an implementation, in order to determine the numerical difference between them. The value of the error metric is the computational error between the data points that are being compared. Computational errors as defined in this International Standard are absolute errors. These are positive numbers and may have units of measure associated with them. When the values being compared are in terms of the same units of measure, there are standard computational error measures based on the Euclidean metric.
In the case of geodetic to geocentric coordinate conversion, a given exact geodetic coordinate (λ, φ, h) corresponds to an exact geocentric coordinate (x, y, z) and both coordinates are assumed to be known. An implementation may use an approximate method for performing the conversion. This results in an approximate geocentric coordinate (xa, ya, za). The error in the conversion is then given directly in metres by
![]() .
.
Sometimes the data that is being compared involves a mixture of measurement units, such as metres and radians, and the process for determining the computational error should be designed to handle such cases.
SRF operations will sometimes result in an approximate coordinate whose components are in terms of both units of distance and angles. In the case of geocentric to geodetic coordinate conversion, a given exact geocentric coordinate (x, y, z) corresponds to an exact geodetic coordinate ( λ, φ, h), where both points are assumed to be known. An implementation may use an approximate method for performing an SRF operation. In such a case the resulting approximate geodetic coordinate is (λa, φa, ha) which involves a mixture of units. However, the computational error can be converted to a distance or position error. This is done to sufficient accuracy as the following typical situation.
Given a reference or true coordinate (λ, φ, h) at a point P and an approximation to this coordinate (λa, φa, ha) located at the point Pa computational error in position is given by the following process.
For an oblate ellipsoid the following relationships hold:
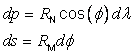
where ds and dp are incremental distances (arc lengths) due to an incremental change in λ and φ [RAPP1]. In particular, ds is the incremental change in arc length along a meridian through P caused by an incremental change dφ in φ., while dp is the incremental change in length of the parallel passing through P caused by an incremental change dλ in λ. For P and Pa sufficiently close together the following relations apply,

with these relationships becoming more exact as Pa approaches P. The computational error E due to converting or transforming from P to Pa is given in metres by,
![]()
or equivalently
![]() .
.
When the conversion or transformation is 2D the same formulation applies with the term in h set to zero.
The determination of computational error in this International Standard is applicable for a single spatial reference frame operation. While the error in a chain of spatial reference frame operations can be determined by a similar procedure this is not addressed in this International Standard.
In some SRF operations, such as computing the convergence of the meridian or computing azimuth, the computed result is a single scalar value ba. In this case, If b is the reference or true value and ba is the computed value, the computational error in radians is
![]() .
.
In the case of point distortion, the variable is a dimensionless ratio, so that the computational error made in computing ka for a reference or true value k is the dimensionless value:
![]() .
.
I.7 Computational error evaluated over test data sets
The previous clause develops the concept of an error metric that can be used to compare data points of true or reference data to the corresponding points resulting from an implementation. It is desirable to have the number of test data points to be relatively large and uniformly distributed over the domain of the operation being evaluated. Legacy implementations of coordinate conversions often are often verified by using a set of test points far too small to properly determine the maximum computational error in an implementation. If the set is not large and dense enough, critical points, where the implementation is flawed, may be missed. The description of the size of the test data sets and the spatial distribution of values in the set is an important consideration and is operation-dependent. Clause 10 contains descriptions of the domains specific to each operation. Once the domain is specified, the appropriate error metric over the whole set of values can be evaluated and the maximum computational error estimated (see Annex B for dense testing methods). The maximum computational error may used to determine a level of conformance of a particular implementation.
Methods for determining the computational error over a test data set and estimating the maximum error can include:
a) calculations performed by hand and supported by a calculating device,
b) calculations performed by hand and supported by a calculating device with respect to an existing authoritative data source,
c) an implementation in one or more higher-order languages of the exact formulations in Clause 10 to form a test data set that can be used to compare to corresponding points computed by an implementation.
A particular implementation should not be required to meet the standard at the highest level if this induces unnecessary complexity and cost penalties. In some applications, users may choose to simplify or approximate the formulations to reduce implementation and computational complexity, and in particular to reduce computer processing time. In doing so, they are willing to accept some degradation in accuracy for a particular application domain.
EXAMPLE The implementation of a conversion from a celestiodetic coordinate system to a geodetic coordinate system is tested on the appropriate domain and the maximum computational error is determined to be less than or equal to 1 mm. This implementation is then said to conform to a 1 mm computational error criterion for that conversion process. Another implementation of the same conversion process, with less stringent requirements, would be said to conform to 20 cm computational error if the maximum computational error is less than or equal to 20 cm.
The computational accuracy requirement for the default profile specified in 12.3 is determined by the error bounds and accuracy domain templates contained in the profile specification. Provision is made for registration of profiles having relaxed computational accuracy requirements.