[ Table of contents ]

8 Spatial reference frames

8.1 Introduction

A spatial coordinate system is a means of associating a unique coordinate with a point in object-space. It is defined by binding an abstract CS to a normal embedding (see 8.2). A spatial reference frame is a specification of a spatial coordinate system for a region of object-space (see 8.3). It is formed by the binding of an abstract coordinate system to the normal embedding specified by an ORM for that object. A full specification specifies the CS and the ORM and includes values for CS parameters, if any, and a specification of the region of object-space. Some or all CS parameters may be bound by ORM parameters. In particular, a CS based on an oblate ellipsoid (or sphere) must match the parameters of the oblate ellipsoid (or sphere) RD of the ORM.

A spatial reference frame template is an abstraction of a collection of spatial reference frames that share the same abstract coordinate system, coordinate system parameter binding rules, and similar ORMs that model the same spatial object type (see 8.5). Spatial reference frames may be organized into specified sets so as to form an atlas for a large region of space. This International Standard specifies a collection of spatial reference frame templates, realizations of those templates, and sets of those realizations.

8.2 Spatial coordinate systems

If a normal embedding of position-space into object-space is defined, any abstract CS for a region of that position-space can be used to specify a spatial CS that associates coordinates in coordinate-space to points in object-space. This association is a binding of a CS via a normal embedding. The association is defined as:

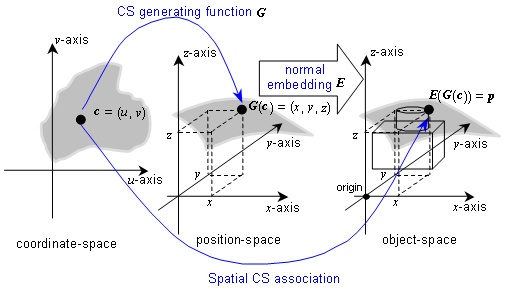
formula or figure

Figure 8.1 — A spatial embedding of a surface CS

EXAMPLE Figure 8.1 illustrates a spatial surface CS bound with a normal embedding of 3D position-space to the 3D object-space. In this illustration, a surface coordinate (u, v) in coordinate-space is associated to a position (x, y, z) in the abstract position-space. That position is then identified with a position in the space of an object via the normal embedding of position-space. In this example, the normal embedding is determined by the selection of an origin and three unit points.

8.3 Spatial reference frame

8.3.1 Specification

A spatial reference frame (SRF) is a specification of a spatial coordinate system that is constructed from an ORM and a compatible abstract CS, such that coordinates uniquely specify positions with respect to the spatial object of the ORM. A specification of an SRF includes:

a) an ORM,

b) a CS compatible with the ORM,

c) a binding of all parameters of the spatial CS,

d) (optionally) k^th coordinate-component names,

e) (optionally) additional restrictions on the domain of valid coordinates in that spatial CS, and

f) (optionally) if the CS is of CS type 3D, a vertical coordinate-component identification (see 8.4).

An SRF implicitly specifies a spatial CS defined by the binding of the CS via the normal embedding associated with the ORM.

Spatial CS compatibility and the other elements of the specification of an SRF are defined in the following clauses.

8.3.2 SRF specification elements

8.3.2.1 ORM and CS compatibility

The compatible CS type of the CS element of an SRF depends on the dimension of the ORM. The dimension of an ORM is defined as the dimension of the RD components of the specification of the ORM. The compatible CS types by ORM dimension are specified in Table 8.1.

Table 8.1 — Compatible CS types

ORM dimension	Compatible CS types
1D	1D CS
2D	Curve CS 2D CS
3D	Curve CS Surface CS 3D CS

The use of surface CSs or 3D CSs that are based on an oblate ellipsoid (or sphere) are restricted to ORMs that are based on an oblate ellipsoid (or respectively, sphere) RD.

The surface CSs that are based on an oblate ellipsoid (or sphere) are:

a) surface geodetic,

b) surface planetodetic, and

c) all map projections.

The 3D CSs that are based on an oblate ellipsoid (or sphere) are:

a) geodetic 3D, and

b) all augmented map projections.

As a further restriction, some CSs are based on spheres only. CS OBLIQUE_MERCATOR_SPHERICAL has this restriction.

8.3.2.2 CS parameter binding

All CS parameter values must be specified. In the case of a combination of a CS and an ORM based on an oblate ellipsoid (or sphere), the major semi-axis and minor semi-axis (or equivalently, the inverse flattening) (or respectively, sphere radius) of the ORM and CS shall match.

8.3.2.3 Coordinate-component names

A CS specification (see 5.9) includes the coordinate-component symbols with common names (if any). A specification of an SRF may optionally assign SRF-specific names to the k^th coordinate-components. The name assignment shall reflect the common use in the intended application domain.

EXAMPLE For a spherical CS, the assignment of SRF-specific names to the k^th coordinate-components of “right ascension” for λ, “declination” for θ , and “radius” for ρ.

8.3.2.4 Coordinate valid-region

A CS specification (see 5.9) includes the specification of the CS domain and CS range where the generating function (or mapping equations) and its inverse(s) are defined. An SRF specification may further restrict the CS domain. A valid-region is a restriction of the CS domain of the generating function (or mapping equations) for a CS as used in an SRF. An extended valid-region is a second valid-region that contains the first valid-region as a subset. The specification of these restrictions is important for several (SRF specific) reasons:

a) If the ORM is local, the restrictions are used to model, in coordinate-space, the local region of the space of the object.

b) If the CS is a map projection or an augmented map projection, the restrictions are used to bound or otherwise limit distortions (see 5.8.3.1).

c) The SRF may be used in conjunction with other SRFs to form an atlas for a large region (see 8.7 SRF sets). In this case, the restrictions are used to control the pair-wise overlap of the spatial coverage of members of the SRF collection.

d) If the CS generating function (or map projection mapping equations) or the inverse function(s) have been implemented with a numerical approximation, the restrictions are used to control error bounds.

The extended valid-region is used primarily for overlapping regions in forming an atlas as in (c) above. Not all properties of the SRF that are true in the valid-region will necessarily be true in the extended valid-region. In particular, a distortion error bound that holds in the valid-region may not hold in the extended valid-region.

A valid-region may be described and/or specified. A valid-region description is a descriptive statement of the region such as the spatial boundary of a named political entity.

EXAMPLE 1 “The German state of Baden-Wurttemberg” and “The Baltic Sea” are valid-region descriptions.

In this International Standard, a valid-region specification is a finite (or empty) list of coordinate-component constraints of the form:

k^th coordinate-component belongs to a non-empty interval of real numbers.

An extended valid-region specification is a finite (or empty) list of coordinate-component constraints of the form:

k^th coordinate-component belongs to an interval of real numbers, where hasbeen specified and.

Angular coordinate-component intervals shall be evaluated modulo 2p to represent an interval of the unit circle. Thus,

In the case of an SRF with an oblate ellipsoid (or sphere) based ORM, celestiodetic coordinates may be similarly constrained. In particular, valid-region specifications for a map projection based SRF may specify coordinate-component constraints for easting, northing, latitude, and/or longitude. Celestiodetic longitude intervals shall be evaluated modulo 2π. In particular, if the interval limits satisfy, then:

formula or figure

EXAMPLE 2         The SRF is based on a transverse Mercator map projection (see SRFT TRANSVERSE_MERCATOR).
Valid-region specification:                         0 ≤ u ≤ 10 000 000,          0 ≤ v ≤ 500 000
Extended valid-region specification:        -100 < u,                            -100 < v
In this example, and are closed bounded intervals, and and are open semi-bounded intervals.

EXAMPLE 3         The SRF is based on a transverse Mercator map projection (see SRFT TRANSVERSE_MERCATOR).
Valid-region specification:                         -78º ≤ λ < -72º,          0º ≤ θ < 84º
Extended valid-region specification:        -78,5º ≤ λ < -71,5º
In this example, and are left-closed, right-open bounded intervals, as is . is not specified. This indicates that there are no constraints for latitude (except for the CS domain definition) in the extended valid-region specification.

8.4 SRF induced surface spatial reference frame

In the case of an SRF specified with the combination of a 3D ORM and a 3D CS, the 3D CS induces a surface CS on each coordinate-component surface (see 5.5.2). An SRF specification may optionally identify the 3^rd coordinate-component as the vertical coordinate-component for the SRF. In that case, the surface CS induced on the zero-value vertical coordinate-component surface is the induced surface SRF for the specification. The vertical coordinate-component is optionally specified in the coordinate-component name specification element of the SRF.

The CS GEODETIC and the CS PLANETODETIC 3^rd coordinate-components (h: ellipsoidal height), and the 3^rd coordinate-component of any augmented map projection CS (h: ellipsoidal height) are identified in this International Standard as the vertical coordinate-component. When an SRF is specified with any of these 3D CSs, the h = 0 coordinate-component surface coincides with the surface of the oblate ellipsoid (or sphere) RD of the ORM. Any SRF based on these CSs intrinsically specifies the corresponding surface CS on the oblate ellipsoid (or sphere) RD surface.

An SRF realized from the SRF template LOCAL_TANGENT_SPACE_EUCLIDEAN specification (see 8.5.6) or the SRF template LOCAL_TANGENT_SPACE_CYLINDRICAL specification (see 8.5.8), the 3^rd coordinate-component, height, is specified as the vertical coordinate-component. In these cases, the zero-value vertical coordinate-component surface is a plane that is tangent to the oblate ellipsoid (or sphere) RD of the ORM. SRF templates are defined in 8.5.

The zero-value 3^rd coordinate-component surface of an SRF realized from the 3D CS SRF template LOCAL_TANGENT_SPACE_AZIMUTHAL_SPHERICAL specification (see 8.5.7) induces a lococentric surface azimuthal CS on the tangent plane of the SRF. For the purpose of specifying an induced surface reference frame, the 3rd coordinate-component q, depression/elevation angle, is specified as a vertical coordinate. The zero-value vertical coordinate-component surface is a plane that is tangent to the oblate ellipsoid (or sphere) RD of the ORM.

SRF templates that are based on surface CSs that can be induced by a zero-value vertical coordinate-component surface of an SRF based on a 3D CS are not separately specified. The induced surface CS is noted in the corresponding 3D CS based SRF template specification.

NOTE Starting with a 3D SRF, this International Standard identifies surface SRFs on coordinate-component surfaces. The relationship between a surface CS and the 3D CS which induces it is functionally similar to, but conceptually different from, the ISO 19111 concept of compound coordinate reference frame. A compound coordinate reference frame synthesizes a 3D reference frame from a surface and a vertical system. (See also 5.8.6.1 and Clause 9.)

8.5 SRF templates

8.5.1 Introduction

An spatial reference frame template (SRFT) is an abstraction of a collection of SRFs that share the same abstract CS, coordinate component names, CS parameter binding rules, and similar ORMs that model the same spatial object type. An SRF template allows for a consistent derivation of SRFs. It is not necessary that an appropriate SRFT be defined in order to define a new SRF; however in this International Standard all SRFs are derived from SRFTs. The specification elements for SRFTs are defined in Table 8.2.

Table 8.2 — SRFT specification elements

Element	Definition
SRFT label	The label of the SRF template (see 13.2.2).
SRFT code	The code of the SRF template (see 13.2.3).
Short name and description	A short name as published or as commonly known and an optional description.
Object or object type	One or more of: abstract, physical, Earth, planet, satellite, and Sun; and, optionally, additional restrictions.
ORM constraint	Criteria for allowable ORMs.
CS label	The label of a CS of compatible type.
CS coordinate-component names and/or symbols	SRF-specific names and/or symbols for the k^th coordinate-component names and/or symbols. If all coordinate-component names and symbols are the same as the CS, the phrase “Same as the CS.” shall be used. The vertical coordinate-component shall be designated in this specification element if applicable.
Template parameters	CS and RD parameters, if any, and/or SRF parameters that are not specified by a CS parameter binding rule.
CS parameter binding rules	A set of rules for binding for CS parameters and ORM component RD parameters, if any, and/or SRF parameters.
Coordinate valid-region	Optional restriction of the domain of the CS to a valid-region. If a valid-region is specified, optionally an extended valid-region. If both are unspecified, then there are no additional constraints on coordinate validity.
Notes	Optional, additional, non-normative information such as a description of the SRF structure, modelled region, intended use, and/or application domain.
References	The references (see 13.2.5).

This International Standard specifies a collection of SRFTs as identified in Table 8.3. Additional SRFTs may be registered in accordance with Clause 13. Registered SRFs shall be derived only from standardized or registered SRFTs.

Table 8.3 — SRFT directory

CS type	Short name	SRFT label
3D	Celestiocentric	CELESTIOCENTRIC
	Local space rectangular 3D	LOCAL_SPACE_RECTANGULAR_3D
	Celestiodetic	CELESTIODETIC
	Planetodetic	PLANETODETIC
	Local tangent space Euclidean	LOCAL_TANGENT_SPACE_EUCLIDEAN
	Local tangent space azimuthal spherical	LOCAL_TANGENT_SPACE_AZIMUTHAL_SPHERICAL
	Local tangent space cylindrical	LOCAL_TANGENT_SPACE_CYLINDRICAL
	Lococentric Euclidean 3D	LOCOCENTRIC_EUCLIDEAN_3D
	Celestiomagnetic	CELESTIOMAGNETIC
	Equatorial inertial	EQUATORIAL_INERTIAL
	Solar ecliptic	SOLAR_ECLIPTIC
	Solar equatorial	SOLAR_EQUATORIAL
	Solar magnetic ecliptic	SOLAR_MAGNETIC_ECLIPTIC
	Solar magnetic	SOLAR_MAGNETIC_DIPOLE
	Heliospheric Aries ecliptic	HELIOSPHERIC_ARIES_ECLIPTIC
	Heliospheric Earth ecliptic	HELIOSPHERIC_EARTH_ECLIPTIC
	Heliospheric Earth equatorial	HELIOSPHERIC_EARTH_EQUATORIAL
Surface (map projection) and 3D (augmented map projection)	Mercator	MERCATOR
	Oblique Mercator spherical	OBLIQUE_MERCATOR_SPHERICAL
	Transverse Mercator	TRANSVERSE_MERCATOR
	Lambert conformal conic	LAMBERT_CONFORMAL_CONIC
	Polar stereographic	POLAR_STEREOGRAPHIC
	Equidistant cylindrical	EQUIDISTANT_CYLINDRICAL
Surface	Surface celestiodetic (induced)	CELESTIODETIC
	Surface planetodetic (induced)	PLANETODETIC
	Local tangent plane Euclidean (induced)	LOCAL_TANGENT_SPACE_EUCLIDEAN
	Local tangent plane azimuthal (induced)	LOCAL_TANGENT_SPACE_AZIMUTHAL_SPHERICAL
	Local tangent plane polar (induced)	LOCAL_TANGENT_SPACE_CYLINDRICAL
2D	Local space rectangular 2D	LOCAL_SPACE_RECTANGULAR_2D
	Local space azimuthal	LOCAL_SPACE_AZIMUTHAL_2D
	Local space polar	LOCAL_SPACE_POLAR_2D

8.5.2 Celestiocentric SRFT

Celestiocentric SRFs shall be derived from the SRFT specified in Table 8.4.

Table 8.4 — Celestiocentric SRFT

Element	Specification
SRFT label	CELESTIOCENTRIC
SRFT code	1
Short name and description	celestiocentric SRFT The generalization of geocentric spatial reference frames to include non-Earth objects.
Object type	physical
ORM constraint	Shall be derived from any 3D ORM.
CS label	EUCLIDEAN_3D
CS coordinate-component names and/or symbols	The same as the CS.
Template parameters	none
CS parameter binding rules	None (no CS parameters).
Coordinate valid-region	No additional restrictions.
Notes	When the object is Earth, this SRFT is referred to as a geocentric SRFT.
References	[EDM]

8.5.3 Local space rectangular 3D SRFT

Local space rectangular SRFs shall be derived from the SRFT specified in Table 8.5.

Table 8.5 — Local space rectangular 3D SRFT

Element	Specification
SRFT label	LOCAL_SPACE_RECTANGULAR_3D
SRFT code	2
Short name and description	local space rectangular 3D SRFT A 3D Euclidean spatial reference frame for an abstract 3D space.
Object type	3D abstract object.
ORM constraint	Shall be an ORM for a 3D abstract object.
CS label	LOCOCENTRIC_EUCLIDEAN_3D
CS coordinate-component names and/or symbols	The same as the CS.
Template parameters	r = vector direction of forward (forward axis). s = vector direction of up (up axis).
CS parameter binding rules
Coordinate valid-region	No additional restrictions.
Notes	CAD/CAM and other engineering applications.
References	[EDM]

8.5.4 Celestiodetic SRFT

Celestiodetic SRFs shall be derived from the SRFT specified in Table 8.6.

Table 8.6 — Celestiodetic SRFT

Element	Specification
SRFT label	CELESTIODETIC
SRFT code	3
Short name and description	celestiodetic SRFT The generalization of geodetic SRFs to include other planets and ellipsoidal bodies.
Object type	physical
ORM constraint	Shall be derived from: ORMT OBLATE_ELLIPSOID or ORMT SPHERE
CS label	GEODETIC
CS coordinate-component names and/or symbols	The same as the CS. The vertical coordinate-component is ellipsoidal height (h).
Template parameters	none
CS parameter binding rules	CS parameters match RD values. Oblate ellipsoid RD case with major semi-axis a and inverse flattening f ^-1: Sphere RD case with radius r :
Coordinate valid-region	No additional restrictions.
Notes	1) The SURFACE_GEODETIC CS is induced on the oblate ellipsoid (or sphere) RD surface. 2) When the object is Earth, this SRFT is referred to as a geodetic SRFT.
References	[HEIK]

8.5.5 Planetodetic SRFT

Planetodetic SRFs shall be derived from the SRFT specified in Table 8.7.

Table 8.7 — Planetodetic SRFT

Element	Specification
SRFT label	PLANETODETIC
SRFT code	4
Short name and description	planetodetic SRFT Similar to celestiodetic SRFT with reversed direction for longitude.
Object type	planet
ORM constraint	Shall be derived from: ORMT OBLATE_ELLIPSOID or ORMT SPHERE
CS label	PLANETODETIC
CS coordinate names and/or symbols	The same as the CS. The vertical coordinate-component is ellipsoidal height (h).
Template parameters	none
CS parameter binding rules	CS parameters match RD values: Oblate ellipsoid RD case with major semi axis a and inverse flattening f ^-1: Sphere RD case with radius r :
Coordinate valid region	No additional restrictions
Notes	Planetary science applications
References	[RIIC]

8.5.6 Local tangent space Euclidean SRFT

Local tangent space Euclidean SRFs shall be derived from the SRFT specified in Table 8.8. The case with template parameters a = 0 and h₀ = 0 is illustrated in Figure 8.2.

Table 8.8 — Local tangent space Euclidean SRFT

Element	Specification
SRFT label	LOCAL_TANGENT_SPACE_EUCLIDEAN
SRFT code	5
Short name and description	local tangent space Euclidean SRFT Euclidean 3D spatial CS with the zero 3^rd coordinate-component surface that is tangent to the oblate ellipsoid RD and with CS natural origin at the tangent point.
Object type	physical
ORM constraint	Shall be derived from: ORMT OBLATE_ELLIPSOID or ORMT SPHERE
CS label	LOCOCENTRIC_EUCLIDEAN_3D
CS coordinate-component names and/or symbols	u: x (x) v: y (y) w: height (h) is the vertical coordinate-component.
Template parameters
CS parameter binding rules
Coordinate valid-region	No additional restrictions.
Notes	1) The LOCOCENTRIC_SURFACE_EUCLIDEAN CS is induced on the tangent plane surface. 2) The w = -h₀ coordinate-component plane 21 is tangent to the oblate ellipsoid RD at the point with surface celestiodetic coordinate (λ,φ). 3) α is the geodetic azimuth of the v-axis (see Figure 8.2). 4) h₀ is the ellipsoidal height of the CS origin.
References	[EDM]

formula or figure

Figure 8.2 — Local tangent space Euclidean SRFT

8.5.7 Local tangent space azimuthal spherical SRFT

Local tangent space azimuthal spherical SRFs shall be derived from the SRFT specified in Table 8.9.

Table 8.9 — Local tangent space azimuthal spherical SRFT

Element	Specification
SRFT label	LOCAL_TANGENT_SPACE_AZIMUTHAL_SPHERICAL
SRFT code	6
Short name and description	local tangent space azimuthal spherical SRFT Azimuthal spherical spatial CS with the zero 3^rd coordinate-component surface that is tangent to the oblate ellipsoid RD and with CS natural origin at the tangent point.
Object type	physical
ORM constraint	Shall be derived from: ORMT OBLATE_ELLIPSOID or ORMT SPHERE
CS label	LOCOCENTRIC_AZIMUTHAL_SPHERICAL
CS coordinate-component names and/or symbols	The same as the CS. θ: depression/elevation angle, is the vertical coordinate-component.
Template parameters
CS parameter binding rules
Coordinate valid-region	No additional restrictions.
Notes	1) Used in radar localization. 2) h₀ is the ellipsoidal height of the CS origin. 3) α is the geodetic azimuth of the v-axis (see Figure 8.2).
References	[EDM]

8.5.8 Local tangent space cylindrical SRFT

Local tangent space cylindrical SRFs shall be derived from the SRFT specified in Table 8.10.

Table 8.10 — Local tangent space cylindrical SRFT

Element	Specification
SRFT label	LOCAL_TANGENT_SPACE_CYLINDRICAL
SRFT code	7
Short name and description	local tangent space cylindrical SRFT cylindrical spatial CS with the zero 3^rd coordinate-component surface that is tangent to the oblate ellipsoid RD and with CS natural origin at the tangent point.
Object type	physical
ORM constraint	Shall be derived from: ORMT OBLATE_ELLIPSOID or ORMT SPHERE
CS label	LOCOCENTRIC_CYLINDRICAL
CS coordinate-component names and/or symbols
Template parameters
CS parameter binding rules
Coordinate valid-region	No additional restrictions.
Notes	1) The LOCOCENTRIC_SURFACE_POLAR CS is induced on the tangent plane surface. 2) The w = -h₀ coordinate-component plane21 is tangent to the oblate ellipsoid RD at the point with surface celestiodetic coordinate (λ,φ). 3) α is the geodetic azimuth of the v-axis (see Figure 8.2). 4) h₀ is the ellipsoidal height of the CS origin.
References	[EDM]

8.5.9 Lococentric Euclidean 3D SRFT

Lococentric Euclidean 3D SRFs shall be derived from the SRFT specified in Table 8.11.

Table 8.11 — Lococentric Euclidean 3D SRFT

Element	Specification
SRFT label	LOCOCENTRIC _EUCLIDEAN_3D
SRFT code	8
Short name and description	Lococentric Euclidean 3D SRFT Euclidean 3D spatial CS with a localised origin and axes orientations
Object type	Any 3D object
ORM constraint	Shall be derived from any 3D ORM.
CS label	LOCOCENTRIC_EUCLIDEAN_3D
CS coordinate-component names and/or symbols	The same as the CS.
Template parameters	Localization parameters: q: the lococentric origin, r: primary axis direction, and s: secondary axis direction. Constraints: r and s are orthonormal vectors.
CS parameter binding rules	The template parameters are the CS parameters
Coordinate valid-region	No additional restrictions.
Notes	1) A CELESTIOCENTRIC SRFT is special case of an instance of this SRFT with and a physical object. 2) A LOCAL_SPACE_RECTANGULAR_3D SRFT is special case of an instance of this SRFT with and an abstract object. 3) A LOCAL_TANGENT_SPACE_EUCLIDEAN SRFT is special case of an instance of this SRFT with q, r, s, satisfying the SRFT LOCAL_TANGENT_SPACE_EUCLIDEAN CS parameter binding rules and ORM constraint. 4) This SRTF is required for the SRM treatment of directions (see 10.5)
References	[EDM]

8.5.10 Celestiomagnetic SRFT

Celestiomagnetic SRFs shall be derived from the SRFT specified in Table 8.12.

Table 8.12 — Celestiomagnetic SRFT

Element	Specification
SRFT label	CELESTIOMAGNETIC
SRFT code	9
Short name and description	celestiomagnetic SRFT A spherical CS based SRFT aligned with the magnetic dipole of a celestial object.
Object type	A planet or rotating satellite in a solar system with a magnetic dipole axis distinct from its rotational axis.
ORM constraint	Based on ORMT BI_AXIS_ORIGIN_3D and OBRS celestiomagnetic.
CS label	SPHERICAL
CS coordinate-component names and/or symbols	The same as the CS.
Template parameters	none
CS parameter binding rules	none
Coordinate valid-region	No additional restrictions.
Notes	1) See 7.5.8. 2) When the object is Earth, this SRFT is referred to as a geomagnetic SRFT. 3) These SRFs are typically used at radii where the magnetic field is approximated by a dipole.
References	[CRUS]

8.5.11 Equatorial inertial SRFT

Equatorial inertial SRFs shall be derived from the SRFT specified in Table 8.13.

Table 8.13 — Equatorial inertial SRFT

Element	Specification
SRFT label	EQUATORIAL_INERTIAL
SRFT code	10
Short name and description	equatorial Inertial SRFT A spherical CS based SRF aligned with the equator of a planet and the direction to the Sun at the vernal equinox (at a specified epoch).
Object type	A planet in the solar system for which the ecliptic plane is distinct from the equatorial plane.
ORM constraint	Based on ORMT BI_AXIS_ORIGIN_3D and OBRS equatorial_inertial.
CS label	SPHERICAL
CS coordinate-component names and/or symbols	λ : right ascension (ra) θ : declination (dec) ρ : radius or range(r)
Template parameters	none
CS parameter binding rules	none
Coordinate valid-region	No additional restrictions.
Notes	1) See 7.5.2. 2) Star catalogues use right ascension and declination to specify directions.
References	[SEID]

8.5.12 Solar ecliptic SRFT

Solar ecliptic SRFs shall be derived from the SRFT specified in Table 8.14.

Table 8.14 — Solar ecliptic SRFT

Element	Specification
SRFT label	SOLAR_ECLIPTIC
SRFT code	11
Short name and description	solar ecliptic SRFT A spherical CS based SRF aligned with the ecliptic plane of a planet and the direction of the Sun.
Object type	A planet in the solar system.
ORM constraint	Based on ORMT BI_AXIS_ORIGIN_3D and OBRS solar_ecliptic.
CS label	SPHERICAL
CS coordinate-component names and/or symbols	The same as the CS.
Template parameters	none
CS parameter binding rules	none
Coordinate valid-region	No additional restrictions.
Notes	See 7.5.3.
References	[HAPG]

8.5.13 Solar equatorial SRFT

Solar equatorial SRFs shall be derived from the SRFT specified in Table 8.15.

Table 8.15 — Solar equatorial SRFT

Element	Specification
SRFT label	SOLAR_EQUATORIAL
SRFT code	12
Short name and description	solar equatorial SRFT A spherical CS based planet centred SRF aligned with the ecliptic plane and the rotational axis of the Sun.
Object type	A planet in the solar system for which the ecliptic plane is distinct from the equatorial plane.
ORM constraint	Based on ORMT BI_AXIS_ORIGIN_3D and OBRS SOLAR_EQUATORIAL.
CS label	SPHERICAL
CS coordinate-component names and/or symbols	The same as the CS.
Template parameters	none
CS parameter binding rules	none
Coordinate valid-region	No additional restrictions.
Notes	See 7.5.4.
References	[CRUS]

8.5.14 Solar magnetic ecliptic SRFT

Solar magnetic ecliptic SRFs shall be derived from the SRFT specified in Table 8.16.

Table 8.16 — Solar magnetic ecliptic SRFT

Element	Specification
SRFT label	SOLAR_MAGNETIC_ECLIPTIC
SRFT code	13
Short name and description	solar magnetic ecliptic SRFT A Euclidean 3D CS based planet centred SRF aligned with the direction to the Sun and the plane determined by that direction and the magnetic dipole of the planet.
Object type	A planet in the solar system with a magnetic dipole.
ORM constraint	Based on ORMT BI_AXIS_ORIGIN_3D and OBRS SOLAR_MAGNETIC_ECLIPTIC.
CS label	EUCLIDEAN_3D
CS coordinate-component names and/or symbols	The same as the CS.
Template parameters	none
CS parameter binding rules	none
Coordinate valid-region	No additional restrictions.
Notes	1) See 7.5.9. 2) In the case of planet Earth, this STF is also known as a geocentric solar magnetospheric SRF.
References	[CRUS]

8.5.15 Solar magnetic dipole SRFT

Solar magnetic dipole SRFs shall be derived from the SRFT specified in Table 8.17.

Table 8.17 — Solar magnetic dipole SRFT

Element	Specification
SRFT label	SOLAR_MAGNETIC_DIPOLE
SRFT code	14
Short name and description	solar magnetic dipole SRFT A Euclidean 3D CS based planet centred SRF with the z-axis aligned with the magnetic dipole and the xz-plane containing the Sun.
Object type	A planet in the solar system with a magnetic dipole axis distinct from its rotational axis.
ORM constraint	Based on ORMT BI_AXIS_ORIGIN_3D and OBRS SOLAR_MAGNETIC_DIPOLE.
CS label	EUCLIDEAN_3D
CS coordinate-component names and/or symbols	The same as the CS.
Template parameters	none
CS parameter binding rules	none
Coordinate valid-region	No additional restrictions.
Notes	See 7.5.10.
References	[CRUS] , [BHAV]

8.5.16 Heliospheric Aries ecliptic SRFT

Heliospheric Aries ecliptic SRFs shall be derived from the SRFT specified in Table 8.18.

Table 8.18 — Heliospheric Aries ecliptic SRFT

Element	Specification
SRFT label	HELIOSPHERIC_ARIES_ECLIPTIC
SRFT code	15
Short name and description	Heliospheric Aries ecliptic SRFT A spherical CS based Sun centred SRF with zero spherical latitude aligned with the ecliptic plane and zero longitude aligned to the first point of Aries.
Object type	Sun.
ORM constraint	Based on ORMT BI_AXIS_ORIGIN_3D and OBRS heliocentric_ARIES_ecliptic.
CS label	SPHERICAL
CS coordinate-component names and/or symbols	The same as the CS.
Template parameters	none
CS parameter binding rules	none
Coordinate valid-region	No additional restrictions.
Notes	See 7.5.5.
References	[HAPG]

8.5.17 Heliospheric Earth ecliptic SRFT

Heliospheric Earth ecliptic SRFs shall be derived from the SRFT specified in Table 8.19.

Table 8.19 — Heliospheric Earth ecliptic SRFT

Element	Specification
SRFT label	HELIOSPHERIC_EARTH_ECLIPTIC
SRFT code	16
Short name and description	heliospheric Earth ecliptic SRFT A spherical CS based Sun centred SRF with zero spherical latitude aligned with the ecliptic plane and zero longitude aligned to the centre of the Earth.
Object type	Sun.
ORM constraint	Based on ORMT BI_AXIS_ORIGIN_3D and OBRS Heliocentric_Planet_Ecliptic.
CS label	SPHERICAL
CS coordinate-component names and/or symbols	The same as the CS.
Template parameters	none
CS parameter binding rules	none
Coordinate valid-region	No additional restrictions.
Notes	See 7.5.6.
References	[HAPG]

8.5.18 Heliospheric Earth equatorial SRFT

Heliospheric Earth equatorial SRFs shall be derived from the SRFT specified in Table 8.20.

Table 8.20 — Heliospheric Earth equatorial SRFT

Element	Specification
SRFT label	HELIOSPHERIC_EARTH_EQUATORIAL
SRFT code	17
Short name and description	heliospheric Earth equatorial SRFT A spherical CS based Sun centred SRF with zero spherical latitude aligned with the equator of the Sun and zero longitude aligned to the centre of the Earth.
Object type	Sun.
ORM constraint	Based on ORMT BI_AXIS_ORIGIN_3D and OBRS Heliocentric_Planet_Equatorial with respect to Earth.
CS label	SPHERICAL
CS coordinate-component names and/or symbols	The same as the CS.
Template parameters	none
CS parameter binding rules	none
Coordinate valid-region	No additional restrictions.
Notes	See 7.5.7.
References	[HAPG]

8.5.19 Mercator SRFT

Mercator SRFs shall be derived from the SRFT specified in Table 8.21.

Table 8.21 — Mercator SRFT

Element	Specification
SRFT label	MERCATOR
SRFT code	18
Short name and description	Mercator SRFT. A Mercator and augmented Mercator map projection of the oblate or sphere RD component of the ORM.
Object type	physical
ORM constraint	Shall be derived from: ORMT OBLATE_ELLIPSOID or ORMT SPHERE
CS label	MERCATOR
CS coordinate-component names and/or symbols	Same as the CS. h: ellipsoidal height is the vertical coordinate-component.
Template parameters
CS parameter binding rules	CS parameters match RD values: Oblate ellipsoid RD case - Major semi-axis a, Sphere RD case - Radius a,
Coordinate valid-region	No additional restrictions.
Notes	1. The augmented Mercator CS induces the Mercator CS on the zero-value vertical coordinate-component surface (which coincides with the RD surface). 2. True scale (point distortion = 1) may be specified at a given latitude by setting:
References	[SNYD]

8.5.20 Oblique Mercator spherical SRFT

Oblique Mercator spherical SRFs shall be derived from the SRFT specified in Table 8.22.

Table 8.22 — Oblique Mercator spherical SRFT

Element	Specification
SRFT label	OBLIQUE_MERCATOR_SPHERICAL
SRFT code	19
Short name and description	Oblique Mercator SRFT for a sphere ORM. An oblique Mercator and augmented oblique Mercator map projection of the sphere RD component of the ORM.
Object type	physical
ORM constraint	Shall be derived from ORMT SPHERE.
CS label	OBLIQUE_MERCATOR_SPHERICAL
CS coordinate-component names and/or symbols	Same as the CS. h: ellipsoidal height is the vertical coordinate-component.
Template parameters
CS parameter binding rules	The CS parameter R matches the RD value: Radius R = r.
Coordinate valid-region	No additional restrictions.
Notes	The augmented oblique Mercator CS induces the oblique Mercator CS on the zero-value vertical coordinate-component surface (which coincides with the RD surface).
References	[SNYD]

8.5.21 Transverse Mercator SRFT

Transverse Mercator SRFs shall be derived from the SRFT specified in Table 8.23.

Table 8.23 — Transverse Mercator SRFT

Element	Specification
SRFT label	TRANSVERSE_MERCATOR
SRFT code	20
Short name and description	Transverse Mercator SRFT A transverse Mercator and augmented transverse Mercator map projection of the oblate or sphere RD component of the ORM.
Object type	physical
ORM constraint	Shall be derived from: ORMT OBLATE_ELLIPSOID or ORMT SPHERE
CS label	TRANSVERSE_MERCATOR
CS coordinate-component names and/or symbols	Same as the CS. h: ellipsoidal height is the vertical coordinate-component.
Template parameters
CS parameter binding rules	CS parameters match RD values: Oblate ellipsoid RD case - Major semi-axis a, Sphere RD case - Radius a,
Coordinate valid-region	No additional restrictions.
Notes	The augmented transverse Mercator CS induces the transverse Mercator CS on the zero-value vertical coordinate-component surface (which coincides with the RD surface).
References	[SNYD]

8.5.22 Lambert conformal conic SRFT

Lambert conformal conic SRFs shall be derived from the SRFT specified in Table 8.24.

Table 8.24 — Lambert conformal conic SRFT

Element	Specification
SRFT label	LAMBERT_CONFORMAL_CONIC
SRFT code	21
Short name and description	Lambert conformal conic SRFT A Lambert conformal conic and augmented Lambert conformal conic map projection of the oblate or sphere RD component of the ORM.
Object type	physical
ORM constraint	Shall be derived from: ORMT OBLATE_ELLIPSOID or ORMT SPHERE
CS label	LAMBERT_CONFORMAL_CONIC
CS coordinate-component names and/or symbols	Same as the CS. h: ellipsoidal height is the vertical coordinate-component.
Template parameters
CS parameter binding rules	CS parameters match RD values: Oblate ellipsoid RD case - Major semi-axis a, Sphere RD case - Radius a,
Coordinate valid-region	No additional restrictions.
Notes	The augmented Lambert conformal conic CS induces the Lambert conformal conic CS on the zero-value vertical coordinate-component surface (which coincides with the RD surface).
References	[SNYD]

8.5.23 Polar stereographic SRFT

Polar stereographic SRFs shall be derived from the SRFT specified in Table 8.25.

Table 8.25 — Polar stereographic SRFT

Element	Specification
SRFT label	POLAR_STEREOGRAPHIC
SRFT code	22
Short name and description	Polar stereographic SRFT A polar stereographic and augmented polar stereographic map projection of the oblate or sphere RD component of the ORM.
Object type	physical
ORM constraint	Shall be derived from: ORMT OBLATE_ELLIPSOID or ORMT SPHERE
CS label	POLAR_STEREOGRAPHIC
CS coordinate-component names and/or symbols	Same as the CS. h: ellipsoidal height is the vertical coordinate-component.
Template parameters
CS parameter binding rules	CS parameters match RD values: Oblate ellipsoid RD case - Major semi-axis a, Sphere RD case - Radius a,
Coordinate valid-region	No additional restrictions.
Notes	1. The augmented polar stereographic CS induces the polar stereographic CS on the zero-value vertical coordinate-component surface (which coincides with the RD surface). 2. True scale (point distortion = 1) may be specified at a given latitude by setting:
References	[SNYD]

8.5.24 Equidistant cylindrical SRFT

Equidistant cylindrical SRFs shall be derived from the SRFT specified in Table 8.26.

Table 8.26 — Equidistant cylindrical SRFT

Element	Specification
SRFT label	EQUIDISTANT_CYLINDRICAL
SRFT code	23
Short name and description	equidistant cylindrical SRFT A equidistant cylindrical and augmented equidistant cylindrical map projection of the sphere RD component of the ORM.
Object type	physical
ORM constraint	Shall be derived from ORMT OBLATE_ELLIPSOID or ORMT SPHERE.
CS label	EQUIDISTANT_CYLINDRICAL
CS coordinate-component names and/or symbols	Same as the CS. h: ellipsoidal height is the vertical coordinate-component.
Template parameters
CS parameter binding rules	CS parameters match RD values: Oblate ellipsoid RD case - Major semi-axis a, Sphere RD case - Radius a,
Coordinate valid-region	No additional restrictions.
Notes	1. The augmented equidistant cylindrical CS induces the equidistant cylindrical CS on the zero-value vertical coordinate-component surface (which coincides with the RD surface). 2. Longitudinal point distortion may be set to one at a given latitude by setting:
References	[SNYD]

8.5.25 Local space rectangular 2D SRFT

Local space rectangular 2D SRFs shall be derived from the SRFT specified in Table 8.27.

Table 8.27 — Local space rectangular 2D SRFT

Element	Specification
SRFT label	LOCAL_SPACE_RECTANGULAR_2D
SRFT code	24
Short name and description	local space rectangular 2D SRFT A 2D Euclidean spatial reference frame for an abstract 2D space.
Object type	2D abstract object
ORM constraint	Shall be an ORM for a 2D abstract object.
CS label	LOCOCENTRIC_EUCLIDEAN_2D
CS coordinate-component names and/or symbols	The same as the CS.
Template parameters	r = vector direction of forward (forward axis).
CS parameter binding rules
Coordinate valid-region	No additional restrictions.
Notes	CAD/CAM and 2D graphic applications.
References	[EDM]

8.5.26 Local Space azimuthal 2D SRFT

Azimuthal 2D SRFs shall be derived from the SRFT specified in Table 8.28.

Table 8.28 — Local Space azimuthal 2D SRFT

Element	Specification
SRFT label	LOCAL_SPACE_AZIMUTHAL_2D
SRFT code	25
Short name and description	Local space azimuthal 2D SRFT An azimuthal CS based SRF for 2D abstract space.
Object type	Abstract object
ORM constraint	Shall be an ORM for a 2D abstract object.
CS label	AZIMUTHAL
CS coordinate-component names and/or symbols	The same as the CS.
Template parameters	none
CS parameter binding rules	none
Coordinate valid-region	No additional restrictions.
Notes	none
References	[EDM]

8.5.27 Local space Polar 2D SRFT

Polar 2D SRFs shall be derived from the SRFT specified in Table 8.29.

Table 8.29 — Local space Polar 2D SRFT

Element	Specification
SRFT label	LOCAL_SPACE_POLAR_2D
SRFT code	26
Short name and description	Local space polar 2D SRFT A polar CS based SRF for 2D abstract space.
Object type	Abstract object
ORM constraint	Shall be an ORM for a 2D abstract object.
CS label	POLAR
CS coordinate-component names and/or symbols	The same as the CS.
Template parameters	none
CS parameter binding rules	none
Coordinate valid-region	No additional restrictions.
Notes	none
References	[EDM]

8.6 Standardized SRFs

This International Standard specifies a collection of SRFs. These specifications appear in Table 8.32 through Table 8.45. Table 8.31 is a directory of these specifications. These SRFs are each derived from a SRFT. Additional SRFs derived from SRFTs may be registered in accordance with Clause 13.

8.6.1 Introduction

The specification elements for SRFs are defined in Table 8.30.

Table 8.30 — Standardized SRF specification elements

Element	Definition
SRF label	The label of the SRF (see 13.2.2).
SRF code	The code of the SRF (see 13.2.3).
Short name	A short name as published or as commonly known and an optional description.
SRF template	The label of the applicable SRF template.
ORM	The label of the applicable ORM.
Valid-region	Optional restriction of the domain of the CS to a valid-region description and/or a valid-region specification. If a valid-region is specified, optionally, an extended valid-region may be specified. Valid-region specifications and extended valid-region specifications are specified by value or by reference. Terms appearing in the references that are cited for a value shall be enclosed in brackets ( { } ).
Parameter values	The SRF template parameter values specified by value or by reference. If by reference, this specification element shall contain a citation(s) for the SRF template parameters values. Terms appearing in the references that are cited for a value shall be enclosed in brackets ( { } ). Any parameter value that is not specified in the citation(s) shall be specified by value.
Notes	Optional, additional, non-normative information concerning the SRF, such as a description of its structure, modelled region, intended use, and/or application domain.
References	The references (see 13.2.5).

Table 8.31 — Directory of standardized SRFs

Short name	SRF label
British national grid	BRITISH_NATIONAL_GRID_AIRY
UK ordnance survey GRS80 grid.	BRITISH_OSGRS80_GRID
Delaware (US) state plane coordinate system	DELAWARE_SPCS_1993
Geocentric WGS 1984	GEOCENTRIC_WGS_1984
Geodetic Australia 1984	GEODETIC_AUSTRALIA_1984
Geodetic WGS 1984	GEODETIC_WGS_1984
Geodetic north american 1983	GEODETIC_N_AMERICAN_1983
Irish grid	IRISH_GRID_1965
Irish transverse Mercator	IRISH_TRANSVERSE_MERCATOR_1989
Lambert-93	LAMBERT_93
Lambert II étendu (Lambert II wide)	LAMBERT_II_WIDE
Mars planetocentric	MARS_PLANETOCENTRIC_2000
Mars planetodetic	MARS_PLANETOGRAPHIC_2000
Maryland (US) state plane coordinate system	MARYLAND_SPCS_1983

8.6.2 British national grid

Table 8.32 — British national grid SRF

Element	Specification	Element	Specification
SRF label	BRITISH_NATIONAL_GRID_AIRY	SRF code	1
Short name	British national grid. A transverse Mercator projection using the AIRY_1830 ellipsoid.
SRF template	TRANSVERSE_MERCATOR	ORM	OSGB_1936
Valid-region	Valid-region description: Great Britain.
Parameter values	longitude of origin: λ_origin = -2º latitude of origin: φ_origin = 49º central scale: k₀ = 0,999 601 271 7 false easting: u_F = -400 000 m false northing: v_F = 100 000 m
Notes	Also known as the UK national projection.
References	[OSTM, Section 7, "National projection"]

8.6.3 UK ordnance survey GRS80 grid

Table 8.33 — UK ordnance survey GRS80 grid SRF

Element	Specification	Element	Specification
SRF label	BRITISH_OSGRS80_GRID	SRF code	2
Short name	UK ordnance survey GRS80 grid. A transverse Mercator projection using the GRS_1980 ellipsoid.
SRF template	TRANSVERSE_MERCATOR	ORM	ETRS_1989
Valid-region	Valid-region description: Great Britain.
Parameter values	longitude of origin: λ_origin = -2º latitude of origin: φ_origin = 49º central scale: k₀ = 0,999 601 271 7 false easting: u_F = -400 000 m false northing: v_F = 100 000 m
Notes	Also known as the OSGRS80 grid.
References	[OSTM, Section 7, " OSGRS80"]

8.6.4 Delaware (US) state plane coordinate system

Table 8.34 — Delaware (US) state plane coordinate system SRF

Element	Specification	Element	Specification
SRF label	DELAWARE_SPCS_1983	SRF code	3
Short name	Delaware (US) state plane coordinate system
SRF template	TRANSVERSE_MERCATOR	ORM	N_AM_1983
Valid-region	Valid-region description: State of Delaware (US).
Parameter values	longitude of origin: λ_origin = -75º 25’ latitude of origin: φ_origin = 38º central scale: k₀ = 1 - 1/200 000 false easting: u_F = 200 000 m false northing: v_F = 0 m
Notes	The conventional coordinate unit is US survey feet. To convert a coordinate in metres to a grid coordinate in US survey feet, use 1m = (39,37 / 12) US survey feet.
References	[SNYD, Table 8 and Appendix C, "Delaware"]

8.6.5 Geocentric WGS 1984

Table 8.35 — Geocentric WGS 1984 SRF

Element	Specification	Element	Specification
SRF label	GEOCENTRIC_WGS_1984	SRF code	4
Short name	Geocentric WGS 1984
SRF template	CELESTIOCENTRIC	ORM	WGS_1984
Valid-region	Valid-region description: Earth, global.
Parameter values	none
Notes	Mass centred.
References	[83502T, Chapter 2.1]

8.6.6 Geodetic Australia 1984

Table 8.36 — Geodetic Australia 1984 SRF

Element	Specification	Element	Specification
SRF label	GEODETIC_AUSTRALIA_1984	SRF code	5
Short name	Geodetic Australia 1984
SRF template	CELESTIODETIC	ORM	AUSTRALIAN_GEOD_1984
Valid-region	Valid-region description: Australia and Tasmania.
Parameter values	none
Notes	none
References	[CECT]

8.6.7 Geodetic WGS 1984

Table 8.37 — Geodetic WGS 1984 SRF

Element	Specification	Element	Specification
SRF label	GEODETIC_WGS_1984	SRF code	6
Short name	Geodetic WGS 1984
SRF template	CELESTIODETIC	ORM	WGS_1984
Valid-region	Valid-region description: Earth, global.
Parameter values	none
Notes	none
References	[83502T, Chapter 3]

8.6.8 Geodetic north american 1983

Table 8.38 — Geodetic north american 1983 SRF

Element	Specification	Element	Specification
SRF label	GEODETIC_N_AMERICAN_1983	SRF code	7
Short name	Geodetic north american 1983
SRF template	CELESTIODETIC	ORM	N_AM_1983
Valid-region	Valid region description: Continental United States
Parameter values	none
Notes	none
References	[SNYD]

8.6.9 Irish grid

Table 8.39 — Irish grid SRF

Element	Specification	Element	Specification
SRF label	IRISH_GRID_1965	SRF code	8
Short name	Irish grid
SRF template	TRANSVERSE_MERCATOR	ORM	IRELAND_1965
Valid-region	Valid-region description: Ireland.
Parameter values	longitude of origin: λ_origin = -8º latitude of origin: φ_origin = 53º 30’ central scale: k₀ = 1,000 035 false easting: u_F = 200 000 m false northing: v_F = 250 000 m
Notes	The Irish Grid has developed over more than two hundred years and is the coordinate reference system used in Ireland.
References	[IGRID, "The Transverse Mercator Map Projection"]

8.6.10 Irish transverse Mercator

Table 8.40 — Irish transverse Mercator SRF

Element	Specification	Element	Specification
SRF label	IRISH_TRANSVERSE_MERCATOR_1989	SRF code	9
Short name	Irish transverse Mercator
SRF template	TRANSVERSE_MERCATOR	ORM	ETRS_1989
Valid-region	Valid-region description: Ireland.
Parameter values	longitude of origin: λ_origin = -8º latitude of origin: φ_origin = 53º 30’ central scale: k₀ = 0,999 820 false easting: u_F = 600 000 m false northing: v_F = 750 000 m
Notes	A newly derived projection designed for GPS compatibility. The longitude and latitude of origin defined in the Irish Grid are maintained.
References	[NMPI, Table 1, "ITM"]

8.6.11 Lambert-93

Table 8.41 — Lambert-93 SRF

Element	Specification	Element	Specification
SRF label	LAMBERT_93	SRF code	10
Short name	Lambert-93
SRF template	LAMBERT_CONFORMAL_CONIC	ORM	RGF_1993
Valid-region	Valid-region description: France.
Parameter values	First parallel: f₁ = 44º Second parallel: f₂ = 49º Longitude of origin: λ_origin = 3º Latitude of origin: φ_origin = 46º 30’ False easting: u_F = 700 000 m False northing: v_F = 6 600 000 m
Notes	Originally specified in September 1996.
References	[PASG, "Caractéristiques de la projection conique conforme (projection dite de Lambert)"]

8.6.12 Lambert II étendu (Lambert II wide)

Table 8.42 — Lambert II étendu (Lambert II wide) SRF

Element	Specification	Element	Specification
SRF label	LAMBERT_II_WIDE	SRF code	11
Short name	Lambert II étendu (Lambert II wide)
SRF template	LAMBERT_CONFORMAL_CONIC	ORM	NTF_1896_PM_PARIS
Valid-region	Valid-region description: France.
Parameter values	First parallel: f₁ = 45º 53’ 56,108” Second parallel: f₂ = 47º 41’ 45,652” Longitude of origin: λ_origin = 0º Latitude of origin: φ_origin = 46º 48’ False easting: u_F = 600 000 m False northing: v_F = 2 200 000 m
Notes	An extension of Lambert Zone II to cover all of France. Note that the prime meridian of the ORM is Paris (not Greenwich).
References	[LIIE, "Valeurs pour le calcul des coordonnes en projection Lambert de l'ellipsoïde de Clarke 1880 IGN.", "Zone lambert: II étendu"]

8.6.13 Mars planetocentric

Table 8.43 — Mars planetocentric SRF

Element	Specification	Element	Specification
SRF label	MARS_PLANETOCENTRIC_2000	SRF code	12
Short name	Mars planetocentric
SRF template	CELESTIODETIC	ORM	MARS_SPHERE_2000
Valid-region	Valid-region description: Mars, global.
Parameter values	none
Notes	1) Also referred to as "east/'ocentric"; adopted as the basis for current map production by the United States Geological Survey (USGS), National Aeronautics and Space Administration (NASA, US), and the European Space Agency (ESA). 2) Spherical latitude coincides with geodetic latitude.
References	[DUXB]

8.6.14 Mars planetographic

Table 8.44 — Mars planetographic SRF

Element	Specification	Element	Specification
SRF label	MARS_PLANETOGRAPHIC_2000	SRF code	13
Short name	Mars planetodetic
SRF template	PLANETODETIC	ORM	MARS_2000
Valid-region	Valid-region description: Mars, global.
Parameter values	none
Notes	1) Also referred to as "west/'ographic"; used historically for map production. 2) Planetodetic longitude is positive westwards.
References	[DUXB]

8.6.15 Maryland (US) state plane coordinate system

Table 8.45 — Maryland (US) state plane coordinate system SRF

Element	Specification	Element	Specification
SRF label	MARYLAND_SPCS_1983	SRF code	14
Short name	Maryland (US) state plane coordinate system
SRF template	LAMBERT_CONFORMAL_CONIC	ORM	N_AM_1983
Valid-region	Valid-region description: State of Maryland (US).
Parameter values	First parallel: f₁ = 38º 18’ Second parallel: f₂ = 39º 27’ Longitude of origin: λ_origin = -77º Latitude of origin: φ_origin = 37º 50’ False easting: u_F = 400 000 m False northing: v_F = 0 m
Notes	The conventional coordinate unit is US survey feet. To convert a coordinate in metres to a grid coordinate in US survey feet, use 1m = (39,37 / 12) US survey feet.
References	[SNYD, Table 8 and Appendix C, "Maryland"]

8.7 Standardized SRF sets

8.7.1 Introduction

A spatial reference frame set (SRFS) for an ORM is a finite parameterized set of two or more spatial reference frames that:

a) are derived from the same SRF template using the given ORM, and

b) the valid-regions of the set members have non-overlapping interiors.

An SRF set specification may further restrict the ORM constraints of the SRFT. The specification elements for SRF sets are defined in Table 8.46. Specification elements for SRF set members are defined in Table 8.47. Each SRF set member shall have a code. The members of an SRF set member may be labelled. If any member of an SRF set has been assigned a label, all members of the set shall be assigned unique labels. An SRF set may contain a large number of members. In particular, the SRF set GTRS_GLOBAL_COORDINATE_SYSTEM, has more than 49 000 members. In such cases, assigning a label to each set member may provide no additional information beyond that which can be obtained from the corresponding code. For such cases, labels may be omitted. In cases where legacy SRF sets have commonly known and widely used member identifiers, such identifiers may be retained as the label for each set member. In particular, the members of the SRF set UNIVERSAL_TRANSVERSE_MERCATOR are labelled.

SRF set member specifications may be either explicit, with a complete specification given for each individual set member, or implicit, with specifications given in terms of general rules that can be instantiated for each individual member. The SRF sets GTRS_GLOBAL_COORDINATE_SYSTEM and UNIVERSAL_TRANSVERSE_MERCATOR illustrate the implicit specification concept.

This International Standard specifies a collection of SRF sets. These specifications appear in Table 8.49 through Table 8.62. Table 8.48 is a directory of standardised SRF sets. The specified collection is not intended to be exhaustive. It includes national and regional grid systems as exemplars of the SRF set concept. Additional SRF sets may be registered in accordance with Clause 13.

Table 8.46 — SRF set specification elements

Element	Definition
SRF set label	The label of the SRF set (see 13.2.2).
SRF set code	The code of the SRF set (see 13.2.3).
Short name	A short name as published or as commonly known, and an optional description.
SRF template	The label of the applicable SRF template.
ORM constraints	Criteria for allowable ORMs. Specifying a single ORM indicates that only that ORM shall be used.
Coverage description	Optional description of the region corresponding to the union of the valid regions of all of the set members.
SRF set membership	A specification of the parameterization of the set members by listing or parameter algorithm, and valid-region descriptions or valid-region specifications. If valid-region specifications are included, extended valid-region specifications may also be included. References to other specification tables may be used for this purpose (see Table 8.47). Valid-region specifications and extended valid-region specifications are specified by value or by reference. Terms appearing in the references that are cited for a value shall be enclosed in brackets ( { } ).
Notes	An optional description of the structure, modelled region, intended use, and/or application domain of the SRF set.
References	Optional references (see 13.2.5).

The specification elements for an SRF set member is defined in Table 8.47.

Table 8.47 — SRF set member specification elements

Element	Definition
SSM label	The optional label of the SRF set member (see 13.2.2), or "n/a" (see 8.7.1).
SSM code	The code of the SRF set member (see 13.2.3); the set member parameter.
Short name	A short name as published or as commonly known and an optional description.
Valid-region	A valid-region description or specification. Optionally an extended valid-region specification. Valid-region specifications and extended valid-region specifications are specified by value or by reference. Terms appearing in the references that are cited for a value shall be enclosed in brackets ( { } ).
Parameter values	The SRF template parameter values specified by value or by reference. If by reference, this specification element shall contain a citation(s) for the SRF template parameters values. Terms appearing in the references that are cited for a value shall be enclosed in brackets ( { } ). Any parameter value that is not specified in the citation(s) shall be specified by value case.
Notes	Optional, additional, non-normative information concerning the SRF set member.

Table 8.48 — Directory of SRF sets

Short name	SRF set label
Alabama (US) state plane coordinate system.	ALABAMA_SPCS
GTRS global coordinate system (GCS) (Earth).	GTRS_GLOBAL_COORDINATE_SYSTEM
Japan plane coordinate system	JAPAN_RECTANGULAR_PLANE_CS
Lambert NTF	LAMBERT_NTF
Universal polar stereographic (Earth)	UNIVERSAL_POLAR_STEREOGRAPHIC
Universal transverse Mercator (Earth)	UNIVERSAL_TRANSVERSE_MERCATOR
Wisconsin (US) state plane coordinate system	WISCONSIN_SPCS

8.7.2 Alabama (US) state plane coordinate system

Table 8.49 — Alabama (US) state plane coordinate system SRF set

Element	Specification	Element	Specification
SRF set label	ALABAMA_SPCS	SRF set code	1
Short name	Alabama (US) state plane coordinate system.
SRF template	TRANSVERSE_MERCATOR	ORM constraints	ORM N_AM_1983
Coverage description	Valid-region description: State of Alabama (US).
SRF set membership	Specified in Table 8.50.
Notes	1) A set of two localized adjacent SRFs where only one SRF is used for each county in the state and no overlap is allowed. 2) The conventional coordinate unit is US survey feet. To convert a coordinate in metres to a grid coordinate in US survey feet, use 1m = (39,37 / 12) US survey feet.
References	[SNYD, Table 8 and Appendix C, "Alabama" (East and West)], [ALSP]

Table 8.50 — SRF set membership Alabama (US) state plane coordinate system

Element	Specification	Element	Specification
SSM label	WEST_ZONE	SSM code	1
Short name	West zone.
Valid-region	Valid-region description: Counties: Autauga, Baldwin, Bibb, Blount, Butler, Chilton, Choctaw, Clarke, Colbert, Conecuh, Cullman, Dallas, Escambia, Fayette, Franklin, Greene, Hale, Jefferson, Lamar, Lauderdale, Lawrence, Limestone, Lowndes, Marengo, Marion, Mobile, Monroe, Morgan, Perry, Pickens, Shelby, Sumter, Tuscaloosa, Walker, Washington, Wilcox and Winston.
Parameter values	longitude of origin: λ_origin = -87º 30’ latitude of origin: φ_origin = 30º central scale: k₀ = 1 - 1/15 000 false easting: u_F = 600 000 m false northing: v_F =0 m
Notes	none.
SSM label	EAST_ZONE	SSM code	2
Short name	East zone.
Valid-region	Valid-region description: Counties: Barbour, Bullock, Calhoun, Chambers, Cherokee, Clay, Cleburne, Coffee, Coosa, Covington, Crenshaw, Dale, DeKalb, Elmore, Etowah, Geneva, Henry, Houston, Jackson, Lee, Macon, Madison, Marshall, Montgomery, Pike, Randolph, Russell, Saint Clair, Talladega and Tallapoosa.
Parameter values	longitude of origin: λ_origin = -85º 50’ latitude of origin: φ_origin = 30º 30’ central scale: k₀ = 1 - 1/25 000 false easting: u_F = 200 000 m false northing: v_F = 0 m
Notes	none.

8.7.3 GTRS global coordinate system (GCS)

Table 8.51 — GTRS global coordinate system (GCS) SRF set

Element	Specification	Element	Specification
SRF set label	GTRS_GLOBAL_COORDINATE_SYSTEM	SRF set code	2
Short name	GTRS global coordinate system (GCS) (Earth).
SRF template	LOCAL_TANGENT_SPACE_EUCLIDEAN	ORM constraints	A global model ERM such as ORM WGS_1984.
Coverage description	Valid-region description: Earth (complete).
SRF set membership	Specified in Table 8.52.
Notes	A set of 49 896 localized SRFs, each approximately 100 kilometres square, that are identified according to the geotile reference system indexing scheme. The members of this SRF set are known as cells. For much of the RD surface, each cell valid-region covers one arc degree of geodetic latitude by one arc degree of geodetic longitude. However, near the poles, many arc degrees of longitude are grouped together into a single GCS cell since an arc degree of geodetic longitude becomes arbitrarily small near the poles. GCS cells are always one arc degree of geodetic latitude in extent. Within each GCS cell, a false origin offset is provided. The point of tangency is at the centre of the rectangular GCS cell, even if more than one arc degree of geodetic longitude falls within the GCS SRF cell. The SRFT LOCAL_TANGENT_SPACE_EUCLIDEAN azimuth parameter (α) is zero.
References	[I18025, Table 6.11, GTRS_GEOTILE], [BIRK]

Table 8.52 — SRF set membership GTRS global coordinate system (GCS)

Element	Specification	Element	Specification
SSM label	n/a	SSM code	1…49823: As specified in Table 8.53.
Short name	Tile <code>.
Valid-region	Valid-region specification: As specified in Table 8.53 as range from the natural origin Extended valid-region specification: Unrestricted.
Parameter values	Surface geodetic coordinate of the tangent point: As specified in Table 8.53. Azimuth: α = 0 rad. Offset height: h₀ = 0 m. false easting: u_F = -50 000 m. false northing: v_F = -50 000 m.
Notes	none

Table 8.53 — GTRS natural origin and valid-region by code index

Latitude band (Tile size)	Tile code	Surface geodetic coordinate of the tangent point (λ_origin, f_origin)	Valid-region specification
88º-90ºS (1º x 30º)	1 + 12•m + n (m=0,1; n=0,..,11)	(-165º + n•30º, -89,5º + m•1º)	-15º ≤ λ - λ_origin ≤+15º -0,5º ≤ φ - φ_origin ≤+0,5º
86º-88ºS (1º x 15º)	25 + 24•m + n (m=0,1; n=0,..,23)	(-172,5º + n•15º, -87,5º + m•1º)	-7,5º ≤ λ - λ_origin ≤+7,5º -0,5º ≤ φ - φ_origin ≤+0,5º
84º-86ºS (1º x 10º)	73 + 36•m + n (m=0,1; n=0,..,35)	(-175º + n•10º, -85,5º + m•1º)	-5º ≤ λ - λ_origin ≤+5º -0,5º ≤ φ - φ_origin ≤+0,5º
80º-84ºS (1º x 6º)	145 + 60•m + n (m=0,..,3; n=0,..,59)	(-177º + n•6º, -83,5º + m•1º)	-3º ≤ λ - λ_origin ≤+3º -0,5º ≤ φ - φ_origin ≤+0,5º
78º-80ºS (1º x 5º)	385 + 72•m + n (m=0,1; n=0,..,71)	(-177,5º + n•5º, -79,5º + m•1º)	-2,5º ≤ λ - λ_origin ≤+2,5º -0,5º ≤ φ - φ_origin ≤+0,5º
71º-78ºS (1º x 3º)	529 + 120•m + n (m=0,..,6; n=0,..,119)	(-178.5º + n•3º, -77,5º + m•1º)	-1,5º ≤ λ - λ_origin ≤+1,5º -0,5º ≤ φ - φ_origin ≤+0,5º
60º-71ºS (1º x 2º)	1369 + 180•m + n (m=0,..,10; n=0,..,179)	(-179º + n•2º, -70,5º + m•1º)	-1º ≤ λ - λ_origin ≤+1º -0,5º ≤ φ - φ_origin ≤+0,5º
60ºS - 60ºN (1º x 1º)	3349 + 360•m + n (m=0,..,119; n=0,..,359)	(-179,5º + n•1º, -59,5º + m•1º)	-0,5º ≤ λ - λ_origin ≤+0,5º -0,5º ≤ φ - φ_origin ≤+0,5º
71º-60ºN (1º x 2º)	46549 + 180•m + n (m=0,..,10; n=0,..,179)	(-179º + n•2º, 60,5º + m•1º)	-1º ≤ λ - λ_origin ≤+1º -0,5º ≤ φ - φ_origin ≤+0,5º
78º-71ºN (1º x 3º)	48529 + 120•m + n (m=0,..,6; n=0,..,119)	(-178.5º + n•3º, 71,5º + m•1º)	-1,5º ≤ λ - λ_origin ≤+1,5º -0,5º ≤ φ - φ_origin ≤+0,5º
80º-78ºN (1º x 5º)	49369 + 72•m + n (m=0,1; n=0,..,71)	(-177,5º + n•5º, 78,5º + m•1º)	-2,5º ≤ λ - λ_origin ≤+2,5º -0,5º ≤ φ - φ_origin ≤+0,5º
84º-80ºN (1º x 6º)	49513 + 60•m + n (m=0,..,3; n=0,..,59)	(-177º + n•6º, 80,5º + m•1º)	-3º ≤ λ - λ_origin ≤+3º -0,5º ≤ φ - φ_origin ≤+0,5º
86º-84ºN (1º x 10º)	49752 + 36•m + n (m=0,1; n=0,..,35)	(-175º + n•10º, 84,5º + m•1º)	-5º ≤ λ - λ_origin ≤+5º -0,5º ≤ φ - φ_origin ≤+0,5º
88º-86ºN (1º x 15º)	49825 + 24•m + n (m=0,1; n=0,..,23)	(-172,5º + n•15º, 86,5º + m•1º)	-7,5º ≤ λ - λ_origin ≤+7,5º -0,5º ≤ φ - φ_origin ≤+0,5º
90º-88ºN (1º x 30º)	49873 + 12•m + n (m=0,1; n=0,..,11)	(-165º + n•30º, 88,5º + m•1º)	-15º ≤ λ - λ_origin ≤+15º -0,5º ≤ φ - φ_origin ≤+0,5º

8.7.4 Japan plane coordinate system

Table 8.54 — Japan plane coordinate system SRF set

Element	Specification	Element	Specification
SRF set label	JAPAN_RECTANGULAR_PLANE_CS	SRF set code	3
Short name	Japan plane coordinate system
SRF template	TRANSVERSE_MERCATOR	ORM constraints	ORM JGD_2000
Coverage description	Valid-region description: Japan excluding northern territories.
SRF set membership	Specified in Table 8.55.
Notes	1) The coordinate-component ordering convention is: northing first, easting second. 2) A set of nineteen localized SRFs, each limited to 130 km eastward and westward from the central meridian. Valid-regions are described by political regions (cities, prefectures, counties, and/or partitions thereof).
References	[JMLIT]

Table 8.55 — SRF set membership Japan plane coordinate system

Element	Specification	Element	Specification
SSM label	ZONE_I	SSM code	1
Short name	Zone I
Valid-region	Valid region description: Prefectures: Nagasaki, Kagosima(islands, atolls, and reefs in 27º ≤ λ ≤ 32º, 128º18’ ≤ φ ≤ 130º (130º13’ for Amami Islands ))
Parameter values	longitude of origin: λ_origin = +129º 30’ latitude of origin: φ_origin = +33º central scale: k₀ = 0,999 9 False easting: u_F = 0 m False northing: v_F = 0 m
Notes	none
SSM label	ZONE_II	SSM code	2
Short name	Zone II
Valid-region	Valid region description: Prefectures: Hukuoka, Saga, Kumamoto, Oita, Miyazaki, Kagosima( excluding the range in Zone_I)
Parameter values	longitude of origin: λ_origin = +131º latitude of origin: φ_origin = +33º central scale: k₀ = 0,999 9 False easting: u_F = 0 m False northing: v_F = 0 m
Notes	none
SSM label	ZONE_III	SSM code	3
Short name	Zone III
Valid-region	Valid region description: Prefectures: Yamaguti, Simane, Hirosima
Parameter values	longitude of origin: λ_origin = +132º 10’ latitude of origin: φ_origin = +36º central scale: k₀ = 0,999 9 False easting: u_F = 0 m False northing: v_F = 0 m
Notes	none
SSM label	ZONE_IV	SSM code	4
Short name	Zone IV
Valid-region	Valid region description: Prefectures: Kagawa, Ehime, Tokusima, Koti
Parameter values	longitude of origin: λ_origin = +133º 30’ latitude of origin: φ_origin = +33º central scale: k₀ = 0,999 9 False easting: u_F = 0 m. False northing: v_F = 0 m.
Notes	none
SSM label	ZONE_V	SSM code	5
Short name	Zone V
Valid-region	Valid region description: Prefectures: Hyogo, Tottori, Okayama
Parameter values	longitude of origin: λ_origin = +134º 20’ latitude of origin: φ_origin = +36º central scale: k₀ = 0,999 9 False easting: u_F = 0 m False northing: v_F = 0 m
Notes	none
SSM label	ZONE_VI	SSM code	6
Short name	Zone VI
Valid-region	Valid region description: Prefectures: Kyoto, Osaka , Hukui, Siga, Mie, Nara, Wakayama
Parameter values	longitude of origin: λ_origin = +136º 00’ latitude of origin: φ_origin = +36º central scale: k₀ = 0,999 9 False easting: u_F = 0 m False northing: v_F = 0 m
Notes	none
SSM label	ZONE_VII	SSM code	7
Short name	Zone VII
Valid-region	Valid region description: Prefectures: Isikawa, Toyama, Gihu, Aiti
Parameter values	longitude of origin: λ_origin = +137º 10’ latitude of origin: φ_origin = +36º central scale: k₀ = 0,999 9 False easting: u_F = 0 m False northing: v_F = 0 m
Notes	none
SSM label	ZONE_VIII	SSM code	8
Short name	Zone VIII
Valid-region	Valid region description: Prefectures: Niigata, Nagano, Yamanasi, Sizuoka
Parameter values	longitude of origin: λ_origin = +138º 30’ latitude of origin: φ_origin = +36º central scale: k₀ = 0,999 9 False easting: u_F = 0 m False northing: v_F = 0 m
Notes	none
SSM label	ZONE_IX	SSM code	9
Short name	Zone IX
Valid-region	Valid region description: Prefectures: Tokyo(excluding the range in Zone_XIV, Zone_XVIII, and Zone_XIX), Hukusima, Totigi, Ibaraki, Saitama, Tiba, Gunma, Kanagawa
Parameter values	longitude of origin: λ_origin = +139º 50’ latitude of origin: φ_origin = +36º central scale: k₀ = 0,999 9 False easting: u_F = 0 m False northing: v_F = 0 m
Notes	none
SSM label	ZONE_X	SSM code	10
Short name	Zone X
Valid-region	Valid region description: Prefectures: Aomori, Akita, Yamagata, Iwate, Miyagi
Parameter values	longitude of origin: λ_origin = +140º 50’ latitude of origin: φ_origin = +40º central scale: k₀ = 0,999 9 False easting: u_F = 0 m False northing: v_F = 0 m
Notes	none
SSM label	ZONE_XI	SSM code	11
Short name	Zone XI
Valid-region	Valid region description: Cities: Otaru, Hakodate, Date Branch offices: Iburi(only Usu County and Abuta County), Hiyama, Siribesi, Osima
Parameter values	longitude of origin: λ_origin = +140º 15’ latitude of origin: φ_origin = +44º central scale: k₀ = 0,999 9 False easting: u_F = 0 m False northing: v_F = 0 m
Notes	none
SSM label	ZONE_XII	SSM code	12
Short name	Zone XII
Valid-region	Valid region description: Cities: Sapporo, Asahikawa, Wakkanai, Rumoi, Bibai Yuubari, Iwamizawa, Tomakomai, Muroran, Sibetu, Nayoro, Asibetu, Akabira, Mikasa, Takikawa, Sunagawa, Ebetu, Titose, Utasinai, Hukagawa, Monbetu, Hurano, Noboribetu, Eniwa, Kitahirosima, Isikari Branch offices: Isikari, Abasiri(only Monbetu County), Kamikawa, Soya, Hidaka, Iburi(excluding Usu County and Abuta County), Sorati, Rumoi
Parameter values	longitude of origin: λ_origin = +142º 15’ latitude of origin: φ_origin = +44º central scale: k₀ = 0,999 9 False easting: u_F = 0 m False northing: v_F = 0 m
Notes	none
SSM label	ZONE_XIII	SSM code	13
Short name	Zone XIII
Valid-region	Valid region description: Cities: Kitami, Obihiro, Kusiro, Abasiri, Nemuro Branch offices: Nemuro, Kusiro, Abasiri(excluding Monbetu County), Tokati
Parameter values	longitude of origin: λ_origin = +144º 15’ latitude of origin: φ_origin = +44º central scale: k₀ = 0,999 9 False easting: u_F = 0 m False northing: v_F = 0 m
Notes	none
SSM label	ZONE_XIV	SSM code	14
Short name	Zone XIV
Valid-region	Valid region description: Tokyo (λ < 28º, 140º 30’ < φ < 143º 00)
Parameter values	longitude of origin: λ_origin = +142º 00’ latitude of origin: φ_origin = +26º central scale: k₀ = 0,999 9 False easting: u_F = 0 m False northing: v_F = 0 m
Notes	none
SSM label	ZONE_XV	SSM code	15
Short name	Zone XV
Valid-region	Valid region description: Okinawa Prefecture (126º < φ < 130º)
Parameter values	longitude of origin: λ_origin = +127º 30’ latitude of origin: φ_origin = +26º central scale: k₀ = 0,999 9 False easting: u_F = 0 m False northing: v_F = 0 m
Notes	none
SSM label	ZONE_XVI	SSM code	16
Short name	Zone XVI
Valid-region	Valid region description: Okinawa Prefecture (φ < 126º )
Parameter values	longitude of origin: λ_origin = +124º 00’ latitude of origin: φ_origin = +26º central scale: k₀ = 0,999 9 False easting: u_F = 0 m False northing: v_F = 0 m
Notes	none
SSM label	ZONE_XVII	SSM code	17
Short name	Zone XVII
Valid-region	Valid region description: Okinawa Prefecture (130º <φ)
Parameter values	longitude of origin: λ_origin = +131º 00’ latitude of origin: φ_origin = +26º central scale: k₀ = 0,999 9 False easting: u_F = 0 m False northing: v_F = 0 m
Notes	none
SSM label	ZONE_XVIII	SSM code	18
Short name	Zone XVIII
Valid-region	Valid region description: Tokyo (λ < 28º , φ < 140º30’ )
Parameter values	longitude of origin: λ_origin = +136º 00’ latitude of origin: φ_origin = +20º central scale: k₀ = 0,999 9 False easting: u_F = 0 m False northing: v_F = 0 m
Notes	none
SSM label	ZONE_XIX	SSM code	19
Short name	Zone XIX
Valid-region	Valid region description: Tokyo (λ < 28º , 143º < φ )
Parameter values	longitude of origin: λ_origin = +154º 00’ latitude of origin: φ_origin = +26º central scale: k₀ = 0,999 9 False easting: u_F = 0 m False northing: v_F = 0 m
Notes	none

8.7.5 Lambert NTF

Table 8.56 — Lambert NTF SRF set

Element	Specification	Element		Specification
SRF set label	LAMBERT_NTF	SRF set code		4
Short name	Lambert NTF. The Lambert projection-based mapping system for France associated with the NTF.
SRF template	LAMBERT_CONFORMAL_CONIC		ORM constraints	ORM NTF_1896_PM_PARIS
Coverage description	Valid-region description: France.
SRF set membership	Specified in Table 8.57.
Notes	A set of four localized adjacent SRFs where only one SRF is used for each portion of France and no overlap is allowed. The prime meridian for each is Paris, France.
References	[LIIE, "Valeurs pour le calcul des coordonnes en projection Lambert de l'ellipsoïde de Clarke 1880 IGN.", "Zone lambert" (I, II, III, and IV)]

Table 8.57 — SRF set membership Lambert NTF

Element	Specification	Element	Specification
SSM label	ZONE_I	SSM code	1
Short name	Zone I
Valid-region	Valid region specification: -5º ≤ λ ≤ 10º -53,5º ≤ φ < 57º
Parameter values	First parallel: φ₁ = 48º 35’ 54,682” Second parallel: φ₂ = 50º 23’ 45,282” Longitude of origin: λ_origin = 0º Latitude of origin: φ_origin = 49,5º False easting: u_F = 600 000 m False northing: v_F =200 000 m
Notes	The prime meridian is Paris, France.
SSM label	ZONE_II	SSM code	2
Short name	Zone II
Valid-region	Valid region specification: -5º ≤ λ ≤ 10º -50,5º ≤ φ < 53,5º
Parameter values	First parallel: φ₁ = 45º 53’ 56,108” Second parallel: φ₂ = 47º 41’ 45,652” Longitude of origin: λ_origin = 0º Latitude of origin: φ_origin = 46,8º False easting: u_F = 600 000 m False northing: v_F =200 000 m
Notes	The prime meridian is Paris, France.
SSM label	ZONE_III	SSM code	3
Short name	Zone III
Valid-region	Valid region specification: -5º ≤ λ ≤ 10º -47º ≤ φ < 50,5º
Parameter values	First parallel: φ₁ = 43º 11’ 57,449” Second parallel: φ₂ = 44º 59’ 45,938” Longitude of origin: λ_origin = 0º Latitude of origin: φ_origin = 44,1º False easting: u_F = 600 000 m False northing: v_F =200 000 m
Notes	The prime meridian is Paris, France.
SSM label	ZONE_IV	SSM code	4
Short name	Zone IV
Valid-region	Valid region specification: The island of Corsica.
Parameter values	First parallel: φ₁ = 41º 33’ 37,396” Second parallel: φ₂ = 42º 46’ 3,588” Longitude of origin: λ_origin = 0º Latitude of origin: φ_origin = 42º 9’ False easting: u_F = 234 358 m False northing: v_F = 185 861,369 m
Notes	The prime meridian is Paris, France.

8.7.6 Universal polar stereographic

Table 8.58 — Universal polar stereographic (UPS) SRF set

Element	Specification	Element		Specification
SRF set label	UNIVERSAL_POLAR_STEREOGRAPHIC		SRF set code	5
Short name	Universal polar stereographic (UPS) (Earth).
SRF template	POLAR_STEREOGRAPHIC	ORM constraints		A global model ERM such as ORM WGS_1984.
Coverage description	Valid-region specification: φ < -80º or 84º ≤ φ Extended valid-region specification: φ < -79,5º or 83,5º ≤ φ
SRF set membership	Specified in Table 8.59.
Notes	A set of two localized SRFs addressing the north and south polar regions of the Earth. Shares a common boundary with SRFS UNIVERSAL_TRANSVERSE_MERCATOR.
References	[83582, "3-2.4 Specifications of the UPS."]

Table 8.59 — SRF set membership Universal polar stereographic (UPS)

Element	Specification		Element	Specification
SSM label	NORTHERN_POLE.		SSM code	1
Short name	UPS, northern pole.
Valid-region	Valid-region specification: φ ≥ 84º Extended valid-region specification: φ ≥ 83,5º
Parameter values	longitude of origin: λ_origin = +0º latitude of true scale: φ₁ = +90º scale at φ₁: k₁ = 0,994 false easting: u_F = 2 000 000 m. false northing: v_F = 2 000 000 m.
Notes	none
SSM label	SOUTHERN_POLE	SSM code		2
Short name	UPS, southern pole.
Valid-region	Valid-region specification: φ ≤ -80º Extended valid-region specification: φ ≤ -79,5º
Parameter values	longitude of origin: λ_origin = +180º latitude of true scale: φ₁ = -90º scale at φ₁: k₁ = 0,994 false easting: u_F = 2 000 000 m. false northing: v_F = 2 000 000 m.
Notes	none

8.7.7 Universal transverse Mercator

Table 8.60 — Universal transverse Mercator (UTM) SRF set

Element	Specification	Element	Specification
SSM label	UNIVERSAL_TRANSVERSE_MERCATOR	SRF set code	6
Short name	Universal transverse Mercator (UTM) (Earth).
SRF template	TRANSVERSE_MERCATOR	ORM constraints	A global model ERM such as ORM WGS_1984.
Coverage description	Valid-region specification: -80º ≤ φ ≤ 84º Extended valid-region specification: -80,5º < φ ≤ 84,5º
SRF set membership	Specified in Table 8.61.
Notes	A set of 120 localized SRFs, where limited overlap is modelled by extended validity regions in the member SRFs. Shares a common boundary with SRFS UNIVERSAL_POLAR_STEREOGRAPHIC.
References	[83582, "2-3 Specifications of the UTM."]

Table 8.61 — SRF set membership Universal transverse Mercator (UTM)

Element	Specification	Element		Specification
SSM label	“ZONE_” + <code> + “_NORTHERN_HEMISPHERE”, where the “+” symbol shall denote concatenation of character strings	SSM code		1…60
Short name	UTM Zone <code>, Northern hemisphere.
Valid-region	Valid-region specification: (-186º + (<code>)•6º) ≤ λ < (-180º + (<code>)•6º) 0º ≤ φ < 84º Extended valid-region specification: (-186,5º + (<code>)•6º) ≤ λ < (-179,5º + (<code>)•6º) -0,5º ≤ φ < 84,5º
Parameter values	longitude of origin: λ_origin = (-183º + (<code>)•6º) latitude of origin: φ_origin = 0º central scale: k₀ = 0,999 6 false easting: u_F = 500 000 m. false northing: v_F = 0 m.
Notes	none
SSM label	“ZONE_” + (<code> - 60) + “_SOUTHERN_HEMISPHERE”, where the “+” symbol shall denote concatenation of character strings		SSM code	61…120
Short Name	UTM Zone <code>, Southern hemisphere.
Valid-region	Valid-region specification: (-186º + (<code> - 60)•6º) ≤ λ < (-180º + (<code> - 60)•6º) -80º ≤ φ < 0º Extended valid-region specification: (-186,5º + (<code> - 60)•6º) ≤ λ < (-179,5º + (<code> - 60)•6º) -80,5º ≤ φ < 0,5º
Parameter values	longitude of origin: λ_origin = (-183º + (<code> - 60)•6º) latitude of origin: φ_origin = 0º. central scale: k₀ = 0,999 6 false easting: u_F = 500 000 m. false northing: v_F = 10 000 000 m.
Notes	none

8.7.8 Wisconsin (US) state plane coordinate system

Table 8.62 — Wisconsin (US) state plane coordinate system SRF set

Element	Specification	Element	Specification
SRF set label	WISCONSIN_SPCS	SRF set code	7
Short name	Wisconsin (US) state plane coordinate system.
SRF template	LAMBERT_CONFORMAL_CONIC	ORM constraints	ORM N_AM_1983
Coverage description	Valid-region description: State of Wisconsin (US).
SRF set membership	Specified in Table 8.63.
Notes	1) A set of three localized adjacent SRFs where only one SRF is used for each county in the state and no overlap is allowed. 2) The conventional coordinate unit is US survey feet. To convert a coordinate in metres to a grid coordinate in US survey feet, use 1m = (39,37 / 12) US survey feet.
References	[WSCO, "SPC 83" (South, Central, and North)]

Table 8.63 — SRF set membership Wisconsin (US) state plane coordinate

Element	Specification	Element	Specification
SSM label	SOUTH_ZONE	SSM code	1
Short name	South zone
Valid-region	Valid region description: Counties: Adams, Calumet, Columbia, Crawford, Dane, Dodge, Fond Du Lac, Grant, Green Lake, Green, Iowa, Jefferson, Juneau, Kenosha, La Crosse, Lafayette, Manitowoc, Marquette, Milwaukee, Monroe, Ozaukee, Racine, Richland, Rock, Sauk, Sheboygan, Vernon, Walworth, Washington, Waukesha, Waushara, Winnebago
Parameter values	First parallel: φ₁ = 42º 44’ Second parallel: φ₂ = 44º 04’ Longitude of origin: λ_origin = -90º Latitude of origin: φ_origin = 42º False easting: u_F = 600 000 m False northing: v_F = 0 m
Notes	none.
SSM label	CENTRAL_ZONE	SSM code	2
Short name	Central zone
Valid-region	Valid region description: Counties: Barron, Brown, Buffalo, Chippewa, Clark, Door, Dunn, Eau Claire, Jackson, Kewaunee, Langlade, Lincoln, Marathon, Marinette, Menominee, Oconto, Outagamie, Pepin, Pierce, Polk, Portage, Rusk, Shawano, St. Croix,Taylor, Trempealeau, Waupaca, Wood
Parameter values	First parallel: φ₁ = 44º 15’ Second parallel: φ₂ = 45º 30’ Longitude of origin: λ_origin = -90º Latitude of origin: φ_origin = 43º 50’ False easting: u_F = 600 000 m False northing: v_F = 0 m
Notes	none.
SSM label	NORTH_ZONE	SSM code	3
Short name	North zone
Valid-region	Valid region description: Counties: Ashland, Bayfield, Burnett, Douglas, Florence, Forest, Iron, Oneida, Price, Sawyer, Vilas, Washburn
Parameter values	First parallel: φ₁ = 45º 34’ Second parallel: φ₂ = 46º 46’ Longitude of origin: λ_origin = -90º Latitude of origin: φ_origin = 45º 10’ False easting: u_F = 600 000 m False northing: v_F = 0 m
Notes	none.

[ Table of contents ]

21 In ISO 19111 terminology, the tangent plane is an engineering datum.